|
RFFGen
|
|
RFFGen
|
Models for the description of different biologial soft tissues. More...
Files | |
| file | adiposeTissue_SommerHolzapfel.hh |
| Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. | |
| file | muscleTissue_Martins.hh |
| Versions of the muscle model of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. | |
| file | skinTissue_Hendriks.hh |
| Versions of the skin model of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. | |
Functions | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::incompressibleAdiposeTissue_SommerHolzapfel (double cCells, double k1, double k2, double kappa, const Matrix &M, const Matrix &F) |
| Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::incompressibleAdiposeTissue_SommerHolzapfel (const Matrix &M, const Matrix &F) |
| Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::compressibleAdiposeTissue_SommerHolzapfel (double cCells, double k1, double k2, double kappa, double d0, double d1, const Matrix &M, const Matrix &F) |
| Compressible version of the model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::compressibleAdiposeTissue_SommerHolzapfel (double d0, double d1, const Matrix &M, const Matrix &F) |
Compressible version of the model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. Material parameters are taken from the same publication, Table 2, i.e. 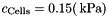 , , 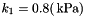 , , 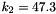 and and 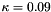 . More... . More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::incompressibleMuscleTissue_Martins (double c, double b, double A, double a, const Matrix &M, const Matrix &F) |
| Incompressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::incompressibleMuscleTissue_Martins (const Matrix &M, const Matrix &F) |
| Incompressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::compressibleMuscleTissue_Martins (double c, double b, double A, double a, double d0, double d1, const Matrix &M, const Matrix &F) |
| Compressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::compressibleMuscleTissue_Martins (double d0, double d1, const Matrix &M, const Matrix &F) |
| Compressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::incompressibleSkin_Hendriks (double c0, double c1, const Matrix &F) |
| Model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::incompressibleSkin_Hendriks (const Matrix &F) |
| Model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::compressibleSkin_Hendriks (double c0, double c1, double d0, double d1, const Matrix &F) |
| Compressible version of the model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | RFFGen::compressibleSkin_Hendriks (double d0, double d1, const Matrix &F) |
| Compressible version of the model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
Models for the description of different biologial soft tissues.
| auto RFFGen::compressibleAdiposeTissue_SommerHolzapfel | ( | double | cCells, |
| double | k1, | ||
| double | k2, | ||
| double | kappa, | ||
| double | d0, | ||
| double | d1, | ||
| const Matrix & | M, | ||
| const Matrix & | F | ||
| ) |
Compressible version of the model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013.
Implementation of the stored energy function 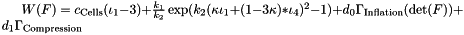 , where
, where 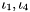 are the first and first mixed invariant of the strain tensor
are the first and first mixed invariant of the strain tensor 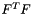 .
.
| cCells | scaling of the neo-Hookean model for the description of the adipocytes as cell foam. |
| k1 | stress-like parameter of the model for the interlobular septa |
| k2 | dimensionless parameter of the model for the interlobular septa |
| kappa | fiber dispersion parameter 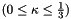 . . |
| M | structural tensor describing the fiber direction of the interlobular septa, i.e. 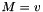 for a fiber direction for a fiber direction 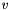 |
| d0 | scaling of the penalty function for inflation |
| d1 | scaling of the penalty function for compression |
| F | initial deformation gradient |
| auto RFFGen::compressibleAdiposeTissue_SommerHolzapfel | ( | double | d0, |
| double | d1, | ||
| const Matrix & | M, | ||
| const Matrix & | F | ||
| ) |
Compressible version of the model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. Material parameters are taken from the same publication, Table 2, i.e. 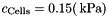 ,
, 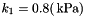 ,
, 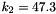 and
and 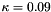 .
.
Implementation of the stored energy function 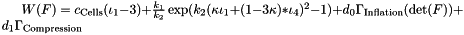 , where
, where 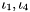 are the first and first mixed invariant of the strain tensor
are the first and first mixed invariant of the strain tensor 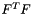 .
.
| d0 | scaling of the penalty function for inflation |
| d1 | scaling of the penalty function for compression |
| M | structural tensor describing the fiber direction of the interlobular septa, i.e. 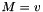 for a fiber direction for a fiber direction 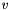 |
| F | initial deformation gradient |
| auto RFFGen::compressibleMuscleTissue_Martins | ( | double | c, |
| double | b, | ||
| double | A, | ||
| double | a, | ||
| double | d0, | ||
| double | d1, | ||
| const Matrix & | M, | ||
| const Matrix & | F | ||
| ) |
Compressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998.
Implementation of the stored energy function 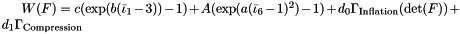 , where
, where 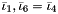 are the first modified principal and the third modified mixed invariant of the strain tensor
are the first modified principal and the third modified mixed invariant of the strain tensor 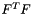 .
.
| c | first material parameter for the isotropic part |
| b | second material parameter for the isotropic part |
| A | first material parameter for the anisotropic part |
| a | second material parameter for the anisotropic part |
| d0 | material parameter for the penalty for inflation |
| d1 | material parameter for the penalty for compression |
| M | structural (rank-one) tensor describing the initial orientation of muscle fibers for 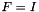 , where , where 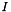 is the unit matrix. is the unit matrix. |
| F | deformation gradient |
| auto RFFGen::compressibleMuscleTissue_Martins | ( | double | d0, |
| double | d1, | ||
| const Matrix & | M, | ||
| const Matrix & | F | ||
| ) |
Compressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998.
Implementation of the stored energy function 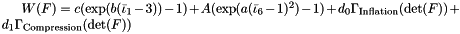 , where
, where 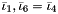 are the first modified principal and the third modified mixed invariant of the strain tensor
are the first modified principal and the third modified mixed invariant of the strain tensor 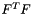 .
.
Material parameters taken from the above mentioned publication, i.e. 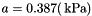 ,
, 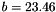 ,
, 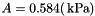 and
and 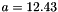 .
.
| d0 | material parameter for the penalty for inflation |
| d1 | material parameter for the penalty for compression |
| M | structural (rank-one) tensor describing the initial orientation of muscle fibers for 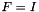 , where , where 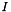 is the unit matrix. is the unit matrix. |
| F | deformation gradient |
| auto RFFGen::compressibleSkin_Hendriks | ( | double | c0, |
| double | c1, | ||
| double | d0, | ||
| double | d1, | ||
| const Matrix & | F | ||
| ) |
Compressible version of the model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005.
Implementation of the stored energy function 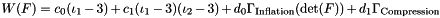 , where
, where 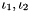 are the first and second principal invariants of the strain tensor
are the first and second principal invariants of the strain tensor 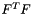 .
.
| c0 | scaling of the shifted first principal invariant |
| c1 | scaling of the product of shifted first and second principal invariant |
| d0 | scaling of the penalty function for inflation |
| d1 | scaling of the penalty function for compression |
| F | initial deformation gradient |
| auto RFFGen::compressibleSkin_Hendriks | ( | double | d0, |
| double | d1, | ||
| const Matrix & | F | ||
| ) |
Compressible version of the model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005.
Implementation of the stored energy function 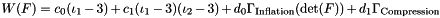 , where
, where 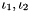 are the first and second principal invariants of the strain tensor
are the first and second principal invariants of the strain tensor 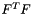 .
.
Material parameters are taken from Xu and Lu: Introduction to Skin Biothermomechanics and Thermal Pain, chapter Skin Biomechanics Modeling, pages 154-206, Springer and Science Press Beijing, 2011, i.e 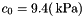 and
and 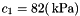 .
.
| d0 | scaling of the penalty function for inflation |
| d1 | scaling of the penalty function for compression |
| F | initial deformation gradient |
| auto RFFGen::incompressibleAdiposeTissue_SommerHolzapfel | ( | double | cCells, |
| double | k1, | ||
| double | k2, | ||
| double | kappa, | ||
| const Matrix & | M, | ||
| const Matrix & | F | ||
| ) |
Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013.
Implementation of the stored energy function 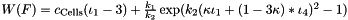 , where
, where 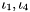 are the first and first mixed invariant of the strain tensor
are the first and first mixed invariant of the strain tensor 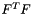 .
.
| cCells | scaling of the neo-Hookean model for the description of the adipocytes as cell foam. |
| k1 | stress-like parameter of the model for the interlobular septa |
| k2 | dimensionless parameter of the model for the interlobular septa |
| kappa | fiber dispersion parameter 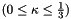 . . |
| M | structural tensor describing the fiber direction of the interlobular septa, i.e. 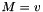 for a fiber direction for a fiber direction 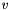 |
| F | initial deformation gradient |
| auto RFFGen::incompressibleAdiposeTissue_SommerHolzapfel | ( | const Matrix & | M, |
| const Matrix & | F | ||
| ) |
Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013.
Implementation of the stored energy function 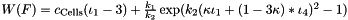 , where
, where 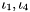 are the first and first mixed invariant of the strain tensor
are the first and first mixed invariant of the strain tensor 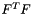 .
.
Material parameters are taken from the above mentioned publication, Table 2, i.e. 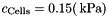 ,
, 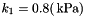 ,
, 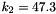 and
and 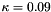 .
.
| M | structural tensor describing the fiber direction of the interlobular septa, i.e. 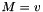 for a fiber direction for a fiber direction 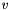 |
| F | initial deformation gradient |
| auto RFFGen::incompressibleMuscleTissue_Martins | ( | double | c, |
| double | b, | ||
| double | A, | ||
| double | a, | ||
| const Matrix & | M, | ||
| const Matrix & | F | ||
| ) |
Incompressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998.
Implementation of the stored energy function 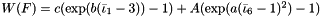 , where
, where 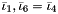 are the first modified principal and the third modified mixed invariant of the strain tensor
are the first modified principal and the third modified mixed invariant of the strain tensor 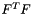 .
.
| c | first material parameter for the isotropic part |
| b | second material parameter for the isotropic part |
| A | first material parameter for the anisotropic part |
| a | second material parameter for the anisotropic part |
| M | structural (rank-one) tensor describing the initial orientation of muscle fibers for 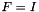 , where , where 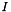 is the unit matrix. is the unit matrix. |
| F | deformation gradient |
| auto RFFGen::incompressibleMuscleTissue_Martins | ( | const Matrix & | M, |
| const Matrix & | F | ||
| ) |
Incompressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998.
Implementation of the stored energy function 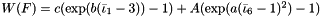 , where
, where 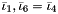 are the first modified principal and the third modified mixed invariant of the strain tensor
are the first modified principal and the third modified mixed invariant of the strain tensor 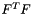 .
.
Material parameters taken from the same above mentioned publication, i.e. 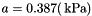 ,
, 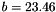 ,
, 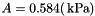 and
and 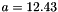 .
.
| M | structural (rank-one) tensor describing the initial orientation of muscle fibers for 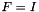 , where , where 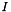 is the unit matrix. is the unit matrix. |
| F | deformation gradient |
| auto RFFGen::incompressibleSkin_Hendriks | ( | double | c0, |
| double | c1, | ||
| const Matrix & | F | ||
| ) |
Model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005.
Implementation of the stored energy function 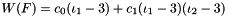 , where
, where 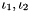 are the first and second principal invariants of the strain tensor
are the first and second principal invariants of the strain tensor 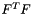 .
.
| c0 | scaling of the shifted first principal invariant |
| c1 | scaling of the product of shifted first and second principal invariant |
| F | initial deformation gradient |
| auto RFFGen::incompressibleSkin_Hendriks | ( | const Matrix & | F | ) |
Model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005.
Implementation of the stored energy function 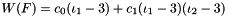 , where
, where 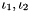 are the first and second principal invariants of the strain tensor
are the first and second principal invariants of the strain tensor 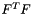 .
.
Material parameters are taken from Xu and Lu: Introduction to Skin Biothermomechanics and Thermal Pain, chapter Skin Biomechanics Modeling, pages 154-206, Springer and Science Press Beijing, 2011, i.e 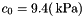 and
and 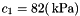 .
.
| F | initial deformation gradient |
 1.8.6
1.8.6