  Checks Checks | Static checks for the presence of different operators and functions |
  CMath CMath | Wrappers for functions from <cmath> |
  LinearAlgebra LinearAlgebra | Functionality from linear algebra such as (modified) principal and mixed matrix invariants |
  MathematicalOperations MathematicalOperations | Mathematical operations and corresponding differentation rules |
  RFFGen RFFGen | Main namespace of the RFFGen library |
   CMath CMath | |
    ASin ASin | Sine function including first three derivatives (based on sin(double) in <cmath>) |
    Cos Cos | Cosine function including first three derivatives (based on cos(double) in <cmath>) |
    Exp Exp | Exponential function including first three derivatives |
    Exp2 Exp2 | Function 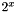 including first three derivatives including first three derivatives |
    LN LN | Natural logarithm including first three derivatives |
    Log10 Log10 | Common (base 10) logarithm including first three derivatives |
    Log2 Log2 | Base 2 logarithm including first three derivatives |
    Pow Pow | Power function with rational exponent 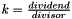 including first three derivatives including first three derivatives |
    Sin Sin | Sine function including first three derivatives (based on sin(double) in <cmath>) |
    Tan Tan | Tangent function including first three derivatives |
   Concepts Concepts | |
    CopyConceptCheck CopyConceptCheck | Static check if the requirements of CopyConcept are satisfied |
    MultiplyWithArithmeticFromLeftConceptCheck MultiplyWithArithmeticFromLeftConceptCheck | Static check if the requirements of MultiplyWithArithmeticFromLeftConcept are satisfied |
    SummationConceptCheck SummationConceptCheck | Static check if the requirements of SummationConcept are satisfied |
    MultiplicationConceptCheck MultiplicationConceptCheck | Static check if the requirements of MultiplicationConcept are satisfied |
    ArithmeticConceptCheck ArithmeticConceptCheck | Static check if the requirements of ArithmeticConcept are satisfied |
    MatrixConceptCheck MatrixConceptCheck | Static check if the requirements of MatrixConcept are satisfied |
    VectorConceptCheck VectorConceptCheck | Static check if the requirements of VectorConcept are satisfied |
    SymmetricMatrixConceptCheck SymmetricMatrixConceptCheck | Static check if the requirements of SymmetricMatrixConcept are satisfied |
    FunctionConceptCheck FunctionConceptCheck | Static check if the requirements of FunctionConcept are satisfied |
    CopyConcept CopyConcept | Requires copy-constructibility and copy-assignability |
    MultiplyWithArithmeticFromLeftConcept MultiplyWithArithmeticFromLeftConcept | Requires that multiplication with double and int can be performed either by in-place multiplication or by multiplication from the left |
    SummationConcept SummationConcept | Requires that summation can be performed either by in-place summation or free summation |
    MultiplicationConcept MultiplicationConcept | Requires that multiplication can be performed |
    ArithmeticConcept ArithmeticConcept | Requirements on input types |
    MatrixConcept MatrixConcept | Requirements for matrices |
    VectorConcept VectorConcept | Requirements for vectors |
    SymmetricMatrixConcept SymmetricMatrixConcept | Requirements for symmetric matrices |
    FunctionConcept FunctionConcept | Minimal requirements for functions |
   LinearAlgebra LinearAlgebra | |
    DynamicSizeDeterminant DynamicSizeDeterminant | Determinant of dynamic size matrix with first three derivatives |
    Deviator Deviator | Type of the deviator of a matrix 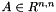 , i.e. , i.e. 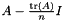 |
    SquaredEuclideanNorm SquaredEuclideanNorm | Compute squared matrix norm 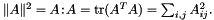 |
    NumberOfRows NumberOfRows | Specialize this for your matrix class. Number of rows must be provided by a static member variable called value |
    NumberOfColumns NumberOfColumns | Specialize this for your matrix class. Number of columns must be provided by a static member variable called value |
    NumberOfRows< Matrix< T, n, m...>, MatrixConceptCheck > NumberOfRows< Matrix< T, n, m...>, MatrixConceptCheck > | Specialization for vectors |
    NumberOfRows< Matrix< T, n, m >, MatrixConceptCheck > NumberOfRows< Matrix< T, n, m >, MatrixConceptCheck > | Specialization for matrices |
    NumberOfRows< Matrix< n, m >, MatrixConceptCheck > NumberOfRows< Matrix< n, m >, MatrixConceptCheck > | Specialization for matrices |
    NumberOfRows< Vector< T, n >, MatrixConceptCheck > NumberOfRows< Vector< T, n >, MatrixConceptCheck > | Specialization for vectors |
    NumberOfRows< Vector< n >, MatrixConceptCheck > NumberOfRows< Vector< n >, MatrixConceptCheck > | Specialization for vectors |
    NumberOfColumns< Matrix< T, n, m >, MatrixConceptCheck > NumberOfColumns< Matrix< T, n, m >, MatrixConceptCheck > | Specialization for matrices |
    NumberOfColumns< Matrix< T, n, m, other...>, MatrixConceptCheck > NumberOfColumns< Matrix< T, n, m, other...>, MatrixConceptCheck > | Specialization for matrices |
    NumberOfColumns< Matrix< n, m >, MatrixConceptCheck > NumberOfColumns< Matrix< n, m >, MatrixConceptCheck > | Specialization for matrices |
    InvariantTraits< Invariant::PRINCIPAL > InvariantTraits< Invariant::PRINCIPAL > | Traits class for access of (shifted) principal invariants |
    InvariantTraits< Invariant::MODIFIED > InvariantTraits< Invariant::MODIFIED > | Traits class for access of (shifted) modified principal invariants |
    InvariantTraits< Invariant::MIXED > InvariantTraits< Invariant::MIXED > | Traits class for access of (shifted) mixed invariants |
    InvariantTraits< Invariant::MODIFIED_MIXED > InvariantTraits< Invariant::MODIFIED_MIXED > | Traits class for access of (shifted) modified mixed invariants |
    SquaredMatrixNorm SquaredMatrixNorm | Compute squared matrix norm 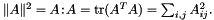 |
    FirstModifiedMixedInvariant FirstModifiedMixedInvariant | First modified mixed invariant 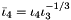 |
    SecondModifiedMixedInvariant SecondModifiedMixedInvariant | Second modified mixed invariant 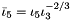 |
    ThirdModifiedMixedInvariant ThirdModifiedMixedInvariant | Third modified mixed invariant 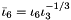 |
    FirstModifiedPrincipalInvariant FirstModifiedPrincipalInvariant | Isochoric (volume-preserving), first modified principal invariant 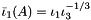 , where , where 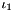 is the first and is the first and 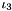 is the third principal invariant is the third principal invariant |
    SecondModifiedPrincipalInvariant SecondModifiedPrincipalInvariant | Isochoric (volume-preserving), second modified principal invariant 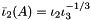 , where , where 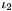 is the second and is the second and 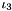 is the third principal invariant is the third principal invariant |
    SecondPrincipalInvariant SecondPrincipalInvariant | Second principal invariant 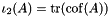 for for 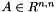 |
    ShiftedInvariant ShiftedInvariant | Possibly scaled, shifted invariant 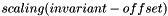 , where , where 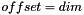 for the first two (principal,modified) invariants and for the first two (principal,modified) invariants and 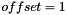 for the third (principal,modified) and mixed invariants for the third (principal,modified) and mixed invariants |
    LeftCauchyGreenStrainTensor LeftCauchyGreenStrainTensor | Left Cauchy-Green strain tensor 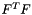 for a symmetric matrix for a symmetric matrix 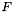 |
    LinearizedStrainTensor LinearizedStrainTensor | Linearized strain tensor 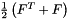 |
    StrainTensor StrainTensor | Strain tensor 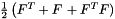 |
   MathematicalOperations MathematicalOperations | |
    Chain Chain | Chain 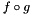 of functions of functions 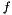 and and 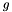 of type F resp. G (F and G must satisfy the requirements of Concepts::FunctionConcept) of type F resp. G (F and G must satisfy the requirements of Concepts::FunctionConcept) |
    Product Product | Product 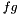 of functions of type F and G (F and G must satisfy the requirements of Concepts::FunctionConcept) of functions of type F and G (F and G must satisfy the requirements of Concepts::FunctionConcept) |
    Scale Scale | Scaling 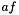 of some function of some function 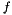 with a double with a double 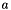 (F must satisfy the requirements of Concepts::FunctionConcept) (F must satisfy the requirements of Concepts::FunctionConcept) |
    Squared Squared | Squared function (F must satisfy the requirements of Concepts::FunctionConcept) |
    Sum Sum | Sum of functions of type F and G (F and G must satisfy the requirements of Concepts::FunctionConcept) |
   Constant Constant | Wrap a constant |
   Identity Identity | Identity mapping 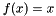 |
   Variable Variable | Independent variable. Can be uniquely identified by its id |
   Base Base | Base class for functions satisfying FunctionConcept. Required for enabling the operators in generate.hh |
   OutOfDomainException OutOfDomainException | Exception for scalar function arguments that are outside the domain of the function |
   NonSymmetricMatrixException NonSymmetricMatrixException | Exception for non-symmetric matrices if symmetric matrices are required |
   Zero Zero | Specialize this struct for your matrix type if a zero matrix cannot be generated via Matrix(0.) |
   Zero< Matrix, void_t< Checks::TryCallToFill< Matrix > > > Zero< Matrix, void_t< Checks::TryCallToFill< Matrix > > > | Specialization for the case that a matrix can be set to zero by calling the member function fill(0) |
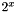 including first three derivatives
including first three derivatives 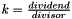 including first three derivatives
including first three derivatives 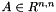 , i.e.
, i.e. 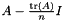
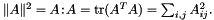
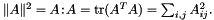
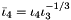
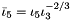
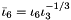
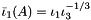 , where
, where 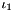 is the first and
is the first and 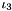 is the third principal invariant
is the third principal invariant 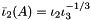 , where
, where 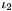 is the second and
is the second and 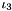 is the third principal invariant
is the third principal invariant 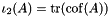 for
for 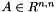
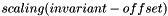 , where
, where 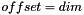 for the first two (principal,modified) invariants and
for the first two (principal,modified) invariants and 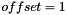 for the third (principal,modified) and mixed invariants
for the third (principal,modified) and mixed invariants 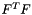 for a symmetric matrix
for a symmetric matrix 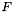
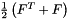
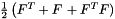
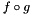 of functions
of functions 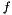 and
and 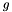 of type F resp. G (F and G must satisfy the requirements of Concepts::FunctionConcept)
of type F resp. G (F and G must satisfy the requirements of Concepts::FunctionConcept) 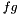 of functions of type F and G (F and G must satisfy the requirements of Concepts::FunctionConcept)
of functions of type F and G (F and G must satisfy the requirements of Concepts::FunctionConcept) 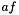 of some function
of some function 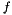 with a double
with a double 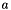 (F must satisfy the requirements of Concepts::FunctionConcept)
(F must satisfy the requirements of Concepts::FunctionConcept) 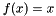
 1.8.6
1.8.6