|
RFFGen
|
Main namespace of the RFFGen library. More...
Classes | |
| struct | Constant |
| Wrap a constant. More... | |
| struct | Identity |
Identity mapping 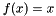 . More... . More... | |
| struct | Variable |
| Independent variable. Can be uniquely identified by its id. More... | |
| struct | Base |
| Base class for functions satisfying FunctionConcept. Required for enabling the operators in generate.hh. More... | |
| class | OutOfDomainException |
| Exception for scalar function arguments that are outside the domain of the function. More... | |
| class | NonSymmetricMatrixException |
| Exception for non-symmetric matrices if symmetric matrices are required. More... | |
| struct | Zero |
| Specialize this struct for your matrix type if a zero matrix cannot be generated via Matrix(0.). More... | |
| struct | Zero< Matrix, void_t< Checks::TryCallToFill< Matrix > > > |
| Specialization for the case that a matrix can be set to zero by calling the member function fill(0). More... | |
Typedefs | |
| template<class F , bool arithmeticArgument = false> | |
| using | Finalize = Detail::FinalizeImpl< F, arithmeticArgument, Checks::hasVariable< F >() > |
| Finish function definition. More... | |
| template<class F , int id> | |
| using | Variable_t = typename VariableDetail::VariableType< F, id >::type |
| Get underlying type of variable with index id. | |
| template<class... Types> | |
| using | void_t = typename Detail::voider< Types...>::type |
| Most fascinating type ever. Is always void. | |
Functions | |
| template<class Arg > | |
| auto | constRef (const Arg &x) |
| Generate a constant function that stores its argument as constant reference. More... | |
| template<class Arg > | |
| auto | constant (const Arg &x) |
| Wrap a constant. More... | |
| template<class F > | |
| auto | finalize (const F &f) |
| Finish function definition. More... | |
| template<class F > | |
| auto | finalize_scalar (const F &f) |
| Finish function definition. More... | |
| template<class F , class G , class = std::enable_if_t< std::is_base_of<Base,F>::value || std::is_base_of<Base,G>::value >> | |
| auto | operator+ (const F &f, const G &g) |
| overload of "+"-operator for the generation of functions. More... | |
| template<class F , class G , class = std::enable_if_t< std::is_base_of<Base,F>::value || std::is_base_of<Base,G>::value >> | |
| auto | operator* (const F &f, const G &g) |
| overload of "*"-operator for the generation of functions. More... | |
| template<class F , class = std::enable_if_t< std::is_base_of<Base,F>::value >> | |
| auto | operator^ (const F &f, int k) |
| overload of "^"-operator for the generation of functions. More... | |
| template<class F , class G , class = std::enable_if_t<std::is_base_of<Base,F>::value && std::is_base_of<Base,G>::value>> | |
| auto | operator<< (const F &f, const G &g) |
overload of "<<"-operator for chaining functions 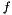 and and 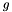 to to 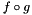 . More... . More... | |
| template<class F , class T , class = std::enable_if_t<std::is_convertible<T,decltype(std::declval<F>().d0())>::value && std::is_base_of<Base,F>::value>> | |
| auto | operator- (const F &f, const T &t) |
| overload of "-"-operator for the generation of functions. Here the second argument is a constant that is wrapped in to an object of type Constant. More... | |
| template<class F , class T , class = std::enable_if_t<std::is_convertible<T,decltype(std::declval<F>().d0())>::value && std::is_base_of<Base,F>::value>> | |
| auto | operator- (const T &t, const F &f) |
| overload of "-"-operator for the generation of functions. Here the first argument is a constant that is wrapped in to an object of type Constant. More... | |
| template<class Arg > | |
| auto | identity (const Arg &x) |
| Construct Identity<Arg>(x). | |
| template<int id, class T > | |
| Variable< T, id > | variable (const T &t) |
| Generate variable from input type. | |
| template<class Inflation , class Compression , class Matrix > | |
| auto | volumetricPenalty (double d0, double d1, const Matrix &A) |
| Create volumetric penalty function composed of a penalty for inflation and one for compression. | |
| template<class Matrix > | |
| auto | volumetricQuadAndLog (double d0, double d1, const Matrix &A) |
Create the volumetric penalty function 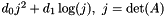 . . | |
| template<class Matrix > | |
| auto | volumetricHartmannNeff (double d0, double d1, const Matrix &A) |
Create the volumetric penalty function 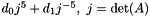 . . | |
| template<class Matrix > | |
| auto | yieldSurface (double beta, double offset, Matrix sigma=LinearAlgebra::unitMatrix< Matrix >()) |
Yield surface 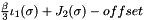 , where , where 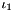 is the first principal and is the first principal and 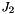 is the second deviatoric invariant. is the second deviatoric invariant. | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleMooneyRivlin (double c0, double c1, const Matrix &F) |
Generate an "incompressible" Mooney-Rivlin material law 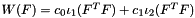 , where , where 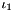 is the first and is the first and 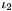 the second principal matrix invariant. the second principal matrix invariant. | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleMooneyRivlin (double c0, double c1, double d0, double d1, const Matrix &F) |
Generate a compressible Mooney-Rivlin material law 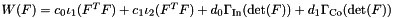 , where , where 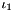 is the first and is the first and 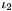 the second principal matrix invariant. the second principal matrix invariant. | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleNeoHooke (double c, const Matrix &F) |
Generate an "incompressible" neo-Hookean material law 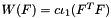 , where , where 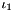 is the first principal matrix invariant . is the first principal matrix invariant . | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | modifiedIncompressibleNeoHooke (double c, const Matrix &F) |
Generate an "incompressible" neo-Hookean material law 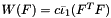 , where , where 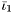 is the modified first principal matrix invariant. is the modified first principal matrix invariant. | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleNeoHooke (double c, double d0, double d1, const Matrix &F) |
Generate a compressible neo-Hookean material law 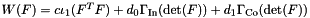 , where , where 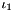 is the first principal matrix invariant. is the first principal matrix invariant. | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | modifiedCompressibleNeoHooke (double c, double d0, double d1, const Matrix &F) |
Generate a compressible neo-Hookean material law 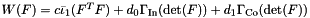 , where , where 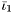 is the modified first principal matrix invariant. is the modified first principal matrix invariant. | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleAdiposeTissue_SommerHolzapfel (double cCells, double k1, double k2, double kappa, const Matrix &M, const Matrix &F) |
| Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleAdiposeTissue_SommerHolzapfel (const Matrix &M, const Matrix &F) |
| Model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleAdiposeTissue_SommerHolzapfel (double cCells, double k1, double k2, double kappa, double d0, double d1, const Matrix &M, const Matrix &F) |
| Compressible version of the model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleAdiposeTissue_SommerHolzapfel (double d0, double d1, const Matrix &M, const Matrix &F) |
Compressible version of the model for adipose tissue of Sommer et al.: Multiaxial mechanical properties and constitutive modeling of human adipose tissue: A basis for preoperative simulations in plastic and reconstructive surgery. Acta Biomater., 9:9036-9048, 2013. Material parameters are taken from the same publication, Table 2, i.e. 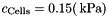 , , 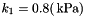 , , 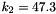 and and 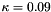 . More... . More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleMuscleTissue_Martins (double c, double b, double A, double a, const Matrix &M, const Matrix &F) |
| Incompressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleMuscleTissue_Martins (const Matrix &M, const Matrix &F) |
| Incompressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleMuscleTissue_Martins (double c, double b, double A, double a, double d0, double d1, const Matrix &M, const Matrix &F) |
| Compressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Inflation , class Compression , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleMuscleTissue_Martins (double d0, double d1, const Matrix &M, const Matrix &F) |
| Compressible version of the model for muscle tissue of Martins et al.: A numerical model of passive and active bahevaior of skeletal muscles. Comp. Meth. Appl. Mech. Eng. 151:419-433, 1998. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleSkin_Hendriks (double c0, double c1, const Matrix &F) |
| Model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | incompressibleSkin_Hendriks (const Matrix &F) |
| Model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleSkin_Hendriks (double c0, double c1, double d0, double d1, const Matrix &F) |
| Compressible version of the model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> | |
| auto | compressibleSkin_Hendriks (double d0, double d1, const Matrix &F) |
| Compressible version of the model for skin tissue of Hendriks: Mechanical behavior of human epidermal and dermal layers in vivo. PhD thesis, Technische Universiteit Eindhoven, 2005. More... | |
| template<class Arg , class = std::enable_if_t< !std::is_base_of<Base,Arg>() && !std::is_arithmetic<Arg>() >, class = std::enable_if_t< !Checks::summation<Arg>() && Checks::inPlaceSummation<Arg>() >> | |
| auto | operator+ (Arg x, const Arg &y) |
| Defines operator+ if not yet defined and in-place summation (operator+=()) is supported. | |
| template<class Arg , class ScalarArg , class = std::enable_if_t< std::is_arithmetic<ScalarArg>::value >, class = std::enable_if_t< !std::is_base_of<Base,Arg>() && !std::is_arithmetic<Arg>() >, class = std::enable_if_t< !Checks::multiplicationWithArithmeticFromLeft<Arg,ScalarArg>() && Checks::inPlaceMultiplicationWithArithmetic<Arg,ScalarArg>() >> | |
| auto | operator* (ScalarArg a, Arg x) |
| Defines operator* for multiplication with built-in arithmetic types from the left if undefined and in-place multiplication (operator*=()) is supported. | |
| template<class Arg , class ScalarArg , class = std::enable_if_t< std::is_arithmetic<ScalarArg>::value >, class = std::enable_if_t< !std::is_base_of<Base,Arg>() && !std::is_arithmetic<Arg>::value>, class = std::enable_if_t< !Checks::multiplicationWithArithmeticFromRight<Arg,ScalarArg>() && Checks::inPlaceMultiplicationWithArithmetic<Arg,ScalarArg>() >> | |
| auto | operator* (Arg x, ScalarArg a) |
| Defines operator* for multiplication with built-in arithmetic types from the right if undefined and in-place multiplication (operator*=()) is supported. | |
| template<class Arg1 , class Arg2 , class = std::enable_if_t< !std::is_base_of<Arg1,Base>() && !std::is_base_of<Arg2,Base>() >, class = std::enable_if_t< !std::is_arithmetic<Arg1>() && !std::is_arithmetic<Arg2>() >, class = std::enable_if_t< !Checks::multiplication<Arg1,Arg2>() && Checks::inPlaceMultiplication<Arg1,Arg2>() >> | |
| auto | operator* (Arg1 x, const Arg2 &y) |
| Defines operator* for multiplication of non-arithmetic types if undefined and in-place multiplication (operator*=()) is supported. | |
| template<class Arg1 , class Arg2 , class = std::enable_if_t< !std::is_base_of<Arg1,Base>() && !std::is_base_of<Arg2,Base>() >, class = std::enable_if_t< !std::is_arithmetic<Arg1>() && !std::is_arithmetic<Arg2>() >, class = std::enable_if_t< !Checks::multiplication<Arg1,Arg2>() && !Checks::inPlaceMultiplication<Arg1,Arg2>() >, class = std::enable_if_t< Checks::callToRightMultiply<Arg1,Arg2>() >> | |
| auto | operator* (Arg1 x, const Arg2 &y) |
| Defines operator* for multiplication of non-arithmetic types if undefined and in-place multiplication is provided in terms of the member function rightmultiplyany() (such as for Dune::FieldMatrix). | |
| template<class Matrix , class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>()>> | |
| Matrix | addTransposed (Matrix &A) |
Overwrites 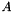 with with 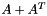 . More... . More... | |
| template<class Matrix , class = std::enable_if_t<!Checks::isConstantSizeMatrix<Matrix>()>, class = std::enable_if_t<Checks::isDynamicMatrix<Matrix>()>> | |
| Matrix | addTransposed (Matrix &A) |
Overwrites 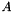 with with 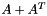 . More... . More... | |
| template<class Matrix , class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>()>> | |
| Matrix | zero () |
| template<class Matrix , class = std::enable_if_t<!Checks::isConstantSizeMatrix<Matrix>()>> | |
| constexpr Matrix | zero (int rows, int cols) |
Main namespace of the RFFGen library.
| using RFFGen::Finalize = typedef Detail::FinalizeImpl< F , arithmeticArgument , Checks::hasVariable<F>() > |
Finish function definition.
Adds the definition of possibly undefined vanishing higher order derivatives.
| Matrix RFFGen::addTransposed | ( | Matrix & | A | ) |
Overwrites 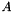 with
with 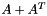 .
.
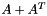
| Matrix RFFGen::addTransposed | ( | Matrix & | A | ) |
Overwrites 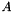 with
with 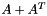 .
.
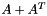
| auto RFFGen::constant | ( | const Arg & | x | ) |
Wrap a constant.
| auto RFFGen::constRef | ( | const Arg & | x | ) |
Generate a constant function that stores its argument as constant reference.
This admits to use variable constant arguments, i.e. parameters that we want to study.
| auto RFFGen::finalize | ( | const F & | f | ) |
Finish function definition.
Adds the definition of possibly undefined vanishing higher order derivatives.
| auto RFFGen::finalize_scalar | ( | const F & | f | ) |
Finish function definition.
Adds the definition of possibly undefined vanishing higher order derivatives.
| auto RFFGen::operator* | ( | const F & | f, |
| const G & | g | ||
| ) |
overload of "*"-operator for the generation of functions.
This is not to be confused with delayed computations with expression templates. This operator is only used to admit intuitive definition of functions. If the resulting type represents a polynomial of order smaller than two, than you need to wrap it into Finalize to generate missing derivatives.
| auto RFFGen::operator+ | ( | const F & | f, |
| const G & | g | ||
| ) |
overload of "+"-operator for the generation of functions.
This is not to be confused with delayed computations with expression templates. This operator is only used to admit intuitive definition of functions. If the resulting type represents a polynomial of order smaller than two, than you need to wrap it into Finalize to generate missing derivatives.
| auto RFFGen::operator- | ( | const F & | f, |
| const T & | t | ||
| ) |
overload of "-"-operator for the generation of functions. Here the second argument is a constant that is wrapped in to an object of type Constant.
This is not to be confused with delayed computations with expression templates. This operator is only used to admit intuitive definition of functions. If the resulting type represents a polynomial of order smaller than two, than you need to wrap it into Finalize to generate missing derivatives.
| auto RFFGen::operator- | ( | const T & | t, |
| const F & | f | ||
| ) |
overload of "-"-operator for the generation of functions. Here the first argument is a constant that is wrapped in to an object of type Constant.
This is not to be confused with delayed computations with expression templates. This operator is only used to admit intuitive definition of functions. If the resulting type represents a polynomial of order smaller than two, than you need to wrap it into Finalize to generate missing derivatives.
| auto RFFGen::operator<< | ( | const F & | f, |
| const G & | g | ||
| ) |
overload of "<<"-operator for chaining functions 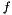 and
and 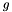 to
to 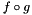 .
.
This is not to be confused with delayed computations with expression templates. This operator is only used to admit intuitive definition of functions. If the resulting type represents a polynomial of order smaller than two, than you need to wrap it into Finalize to generate missing derivatives.
| auto RFFGen::operator^ | ( | const F & | f, |
| int | k | ||
| ) |
overload of "^"-operator for the generation of functions.
This is not to be confused with delayed computations with expression templates. This operator is only used to admit intuitive definition of functions. If the resulting type represents a polynomial of order smaller than two, than you need to wrap it into Finalize to generate missing derivatives.
| Matrix RFFGen::zero | ( | ) |
Requires that a specialization of struct Zero exists for Matrix.
| constexpr Matrix RFFGen::zero | ( | int | rows, |
| int | cols | ||
| ) |
Requires that a specialization of struct Zero exists for Matrix.
 1.8.6
1.8.6