Isotropic models for the description of rubber materials (neo-Hookean and Mooney-Rivlin models). More...

Files
file	mooneyRivlin.hh
	Models based on the Mooney-Rivlin material law. Input argument is the deformation gradient.

file	neoHooke.hh
	Models based on the neo-Hookean material law. Input argument is the deformation gradient.

Functions
template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()>
auto	RFFGen::incompressibleMooneyRivlin (double c0, double c1, const Matrix &F)
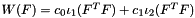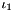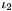	Generate an "incompressible" Mooney-Rivlin material law $W(F)=c_0\iota_1(F^T F) + c_1\iota_2(F^T F)$ , where $\iota_1$ is the first and $\iota_2$ the second principal matrix invariant.

template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()>
auto	RFFGen::compressibleMooneyRivlin (double c0, double c1, double d0, double d1, const Matrix &F)
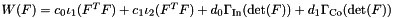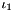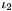	Generate a compressible Mooney-Rivlin material law $W(F)=c_0\iota_1(F^T F) + c_1\iota_2(F^T F) + d_0\Gamma_\mathrm{In}(\det(F))+d_1\Gamma_\mathrm{Co}(\det(F))$ , where $\iota_1$ is the first and $\iota_2$ the second principal matrix invariant.

template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()>
auto	RFFGen::incompressibleNeoHooke (double c, const Matrix &F)
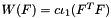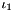	Generate an "incompressible" neo-Hookean material law $W(F)=c\iota_1(F^T F)$ , where $\iota_1$ is the first principal matrix invariant .

template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()>
auto	RFFGen::modifiedIncompressibleNeoHooke (double c, const Matrix &F)
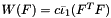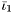	Generate an "incompressible" neo-Hookean material law $W(F)=c\bar\iota_1(F^T F)$ , where $\bar\iota_1$ is the modified first principal matrix invariant.

template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()>
auto	RFFGen::compressibleNeoHooke (double c, double d0, double d1, const Matrix &F)
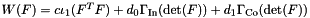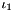	Generate a compressible neo-Hookean material law $W(F)=c\iota_1(F^T F)+d_0\Gamma_\mathrm{In}(\det(F))+d_1\Gamma_\mathrm{Co}(\det(F))$ , where $\iota_1$ is the first principal matrix invariant.

template<class InflationPenalty , class CompressionPenalty , class Matrix , int offset = LinearAlgebra::dimension<Matrix>()>
auto	RFFGen::modifiedCompressibleNeoHooke (double c, double d0, double d1, const Matrix &F)
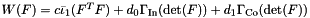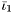	Generate a compressible neo-Hookean material law $W(F)=c\bar\iota_1(F^T F)+d_0\Gamma_\mathrm{In}(\det(F))+d_1\Gamma_\mathrm{Co}(\det(F))$ , where $\bar\iota_1$ is the modified first principal matrix invariant.

Detailed Description

Isotropic models for the description of rubber materials (neo-Hookean and Mooney-Rivlin models).

Files

Functions

Detailed Description