RFFGen::CMath::Pow< dividend, divisor > Struct Template Reference

Power function with rational exponent 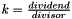including first three derivatives. More...

#include <pow.hh>

Inheritance diagram for RFFGen::CMath::Pow< dividend, divisor >:

Public Member Functions
	Pow (double x=1)
	Constructor. More...
void	update (double x)
	Reset point of evaluation.
double	d0 () const noexcept
	Function value.
template<int = -1>
double	d1 (double dx=1.) const
	First (directional) derivative.
template<int = -1, int = -1>
double	d2 (double dx=1., double dy=1.) const
	Second (directinal) derivative.
template<int = -1, int = -1, int = -1>
double	d3 (double dx=1., double dy=1., double dz=1.) const
	Third (directional) derivative.
Public Member Functions inherited from RFFGen::Base
template<class Arg >
void	update (const Arg &)
	Update on changed input.
template<int id, class Arg >
void	updateVariable (const Arg &)
	Empty variables.

Detailed Description

template<int dividend, int divisor = 1>
struct RFFGen::CMath::Pow< dividend, divisor >

Power function with rational exponent 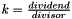including first three derivatives.

For scalar functions directional derivatives are less interesting. Incorporating this function as building block for more complex functions requires directional derivatives. These occur during applications of the chain rule. For the cases 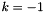and 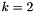specializations are used that avoid the use of std::pow.

Constructor & Destructor Documentation

template<int dividend, int divisor = 1>

RFFGen::CMath::Pow< dividend, divisor >::Pow ( double  x = 1 )

inlineexplicit

Constructor.

Parameters

x	point of evaluation

---

The documentation for this struct was generated from the following file:

• RFFGen/CMath/pow.hh