Matrix Invariants (principal and mixed, modified (isochoric) invariants and deviatoric invariants).
More...
|
| struct | RFFGen::LinearAlgebra::InvariantTraits< Invariant::PRINCIPAL > |
| | Traits class for access of (shifted) principal invariants. More...
|
| |
| struct | RFFGen::LinearAlgebra::InvariantTraits< Invariant::MODIFIED > |
| | Traits class for access of (shifted) modified principal invariants. More...
|
| |
| struct | RFFGen::LinearAlgebra::InvariantTraits< Invariant::MIXED > |
| | Traits class for access of (shifted) mixed invariants. More...
|
| |
| struct | RFFGen::LinearAlgebra::InvariantTraits< Invariant::MODIFIED_MIXED > |
| | Traits class for access of (shifted) modified mixed invariants. More...
|
| |
| struct | RFFGen::LinearAlgebra::FirstModifiedMixedInvariant< Matrix, class > |
| | First modified mixed invariant 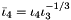 . More... . More...
|
| |
| struct | RFFGen::LinearAlgebra::SecondModifiedMixedInvariant< Matrix, class > |
| | Second modified mixed invariant 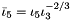 . More... . More...
|
| |
| struct | RFFGen::LinearAlgebra::ThirdModifiedMixedInvariant< Matrix, class > |
| | Third modified mixed invariant 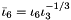 . More... . More...
|
| |
| struct | RFFGen::LinearAlgebra::FirstModifiedPrincipalInvariant< Matrix, class > |
| | Isochoric (volume-preserving), first modified principal invariant 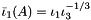 , where , where 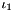 is the first and is the first and 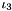 is the third principal invariant. More... is the third principal invariant. More...
|
| |
| struct | RFFGen::LinearAlgebra::SecondModifiedPrincipalInvariant< Matrix, class > |
| | Isochoric (volume-preserving), second modified principal invariant 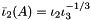 , where , where 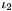 is the second and is the second and 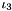 is the third principal invariant. More... is the third principal invariant. More...
|
| |
| class | RFFGen::LinearAlgebra::SecondPrincipalInvariant< Matrix, class > |
| | Second principal invariant 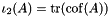 for for 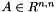 . More... . More...
|
| |
|
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::SecondDeviatoricInvariant = MathematicalOperations::Chain< MatrixNorm< Matrix >, Deviator< Matrix > > |
| | Second deviator invariant 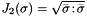 with with 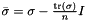 and and 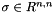 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::FirstMixedInvariant = MathematicalOperations::Chain< FirstPrincipalInvariant< Matrix >, MathematicalOperations::Product< Identity< Matrix >, Constant< Matrix > > > |
| | First mixed invariant 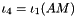 of a matrix of a matrix 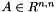 with respect to the structural tensor with respect to the structural tensor 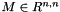 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::SecondMixedInvariant = MathematicalOperations::Chain< FirstPrincipalInvariant< Matrix >, MathematicalOperations::Product< MathematicalOperations::Squared< Identity< Matrix > >, Constant< Matrix > > > |
| | Second mixed invariant 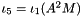 of a matrix of a matrix 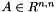 with respect to the structural tensor with respect to the structural tensor 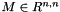 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ThirdMixedInvariant = MathematicalOperations::Chain< FirstPrincipalInvariant< Matrix >, MathematicalOperations::Product< Identity< Matrix >, MathematicalOperations::Squared< Constant< Matrix > > > > |
| | Third mixed invariant 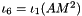 of a matrix of a matrix 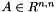 with respect to the structural tensor with respect to the structural tensor 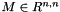 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedFirstMixedInvariant = ShiftedInvariant< FirstMixedInvariant< Matrix >, 1 > |
| | Shifted first mixed invariant 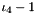 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedSecondMixedInvariant = ShiftedInvariant< SecondMixedInvariant< Matrix >, 1 > |
| | Shifted second mixed invariant 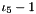 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedThirdMixedInvariant = ShiftedInvariant< ThirdMixedInvariant< Matrix >, 1 > |
| | Shifted third mixed invariant 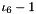 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedFirstModifiedMixedInvariant = ShiftedInvariant< FirstModifiedMixedInvariant< Matrix >, 1 > |
| | Shifted first modified mixed invariant 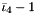 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedSecondModifiedMixedInvariant = ShiftedInvariant< SecondModifiedMixedInvariant< Matrix >, 1 > |
| | Shifted second modified mixed invariant 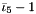 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedThirdModifiedMixedInvariant = ShiftedInvariant< ThirdModifiedMixedInvariant< Matrix >, 1 > |
| | Shifted third modified mixed invariant 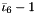 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ThirdModifiedPrincipalInvariant = ThirdPrincipalInvariant< Matrix > |
| | Third modified principal invariant is the same as the third principal invariant. This invariant describes volumetric changes.
|
| |
|
template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> |
| using | RFFGen::LinearAlgebra::ShiftedFirstModifiedPrincipalInvariant = ShiftedInvariant< FirstModifiedPrincipalInvariant< Matrix >, offset > |
| | Shifted first modified principal invariant 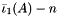 for for 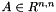 . .
|
| |
|
template<class Matrix , int offset = LinearAlgebra::dimension<Matrix>()> |
| using | RFFGen::LinearAlgebra::ShiftedSecondModifiedPrincipalInvariant = ShiftedInvariant< SecondModifiedPrincipalInvariant< Matrix >, offset > |
| | Shifted second modified principal invariant 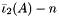 for for 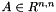 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedThirdModifiedPrincipalInvariant = ShiftedInvariant< ThirdModifiedPrincipalInvariant< Matrix >, 1 > |
| | Shifted third modified principal invariant 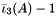 for for 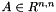 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::FirstPrincipalInvariant = Trace< Matrix > |
| | First principal invariant 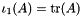 for for 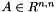 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ThirdPrincipalInvariant = Determinant< Matrix > |
| | Third principal invariant 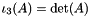 for for 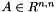 . .
|
| |
|
template<class Matrix , int offset = dimension<Matrix>()> |
| using | RFFGen::LinearAlgebra::ShiftedFirstPrincipalInvariant = ShiftedInvariant< FirstPrincipalInvariant< Matrix >, offset > |
| | Shifted first principal invariant 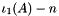 for for 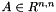 . .
|
| |
|
template<class Matrix , int offset = dimension<Matrix>()> |
| using | RFFGen::LinearAlgebra::ShiftedSecondPrincipalInvariant = ShiftedInvariant< SecondPrincipalInvariant< Matrix >, offset > |
| | Shifted second principal invariant 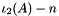 for for 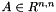 . .
|
| |
|
template<class Matrix > |
| using | RFFGen::LinearAlgebra::ShiftedThirdPrincipalInvariant = ShiftedInvariant< ThirdPrincipalInvariant< Matrix >, 1 > |
| | Shifted third principal invariant 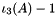 for for 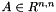 . .
|
| |
Matrix Invariants (principal and mixed, modified (isochoric) invariants and deviatoric invariants).
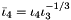 . More...
. More...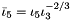 . More...
. More...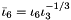 . More...
. More...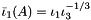 , where
, where 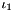 is the first and
is the first and 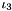 is the third principal invariant. More...
is the third principal invariant. More...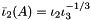 , where
, where 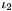 is the second and
is the second and 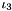 is the third principal invariant. More...
is the third principal invariant. More...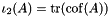 for
for 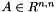 . More...
. More...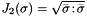 with
with 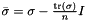 and
and 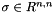 .
. 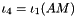 of a matrix
of a matrix 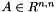 with respect to the structural tensor
with respect to the structural tensor 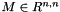 .
. 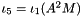 of a matrix
of a matrix 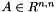 with respect to the structural tensor
with respect to the structural tensor 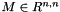 .
. 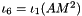 of a matrix
of a matrix 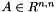 with respect to the structural tensor
with respect to the structural tensor 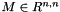 .
. 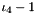 .
. 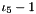 .
. 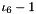 .
. 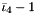 .
. 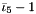 .
. 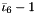 .
. 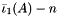 for
for 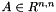 .
. 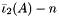 for
for 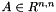 .
. 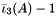 for
for 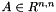 .
. 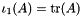 for
for 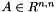 .
. 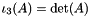 for
for 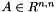 .
. 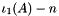 for
for 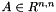 .
. 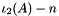 for
for 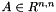 .
. 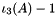 for
for 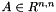 .
.  1.8.6
1.8.6