|
RFFGen
|
|
RFFGen
|
Functionality from linear algebra such as (modified) principal and mixed matrix invariants. More...
Modules | |
| Invariants | |
| Matrix Invariants (principal and mixed, modified (isochoric) invariants and deviatoric invariants). | |
Namespaces | |
| LinearAlgebra | |
| Functionality from linear algebra such as (modified) principal and mixed matrix invariants. | |
Classes | |
| class | RFFGen::LinearAlgebra::DynamicSizeDeterminant< Matrix > |
| Determinant of dynamic size matrix with first three derivatives. More... | |
| class | RFFGen::LinearAlgebra::Deviator< Matrix > |
Type of the deviator of a matrix 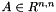 , i.e. , i.e. 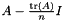 . More... . More... | |
| struct | RFFGen::LinearAlgebra::SquaredEuclideanNorm< Matrix, class > |
Compute squared matrix norm 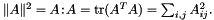 . More... . More... | |
| struct | RFFGen::LinearAlgebra::SquaredMatrixNorm< Matrix, class > |
Compute squared matrix norm 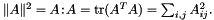 . More... . More... | |
| class | RFFGen::LinearAlgebra::ShiftedInvariant< Invariant, offset > |
Possibly scaled, shifted invariant 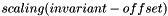 , where , where 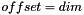 for the first two (principal,modified) invariants and for the first two (principal,modified) invariants and 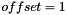 for the third (principal,modified) and mixed invariants. More... for the third (principal,modified) and mixed invariants. More... | |
| class | RFFGen::LinearAlgebra::LeftCauchyGreenStrainTensor< Matrix, class > |
Left Cauchy-Green strain tensor 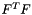 for a symmetric matrix for a symmetric matrix 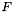 . More... . More... | |
| class | RFFGen::LinearAlgebra::LinearizedStrainTensor< Matrix, class > |
Linearized strain tensor 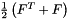 . More... . More... | |
| class | RFFGen::LinearAlgebra::StrainTensor< Matrix > |
Strain tensor 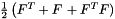 . More... . More... | |
Typedefs | |
| template<class Matrix > | |
| using | RFFGen::LinearAlgebra::ConstantSizeDeterminant = Detail::DeterminantImpl< Matrix, dimension< Matrix >()> |
| Determinant of constant size matrix with first three derivatives. | |
| template<class Matrix > | |
| using | RFFGen::LinearAlgebra::Determinant = std::conditional_t< Checks::isConstantSizeMatrix< Matrix >(), ConstantSizeDeterminant< Matrix >, DynamicSizeDeterminant< Matrix > > |
| Determinant with first three derivatives. | |
| template<class Matrix > | |
| using | RFFGen::LinearAlgebra::EuclideanNorm = MathematicalOperations::Chain< CMath::Sqrt, SquaredEuclideanNorm< Matrix > > |
Compute matrix norm 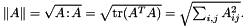 . . | |
| template<class Matrix > | |
| using | RFFGen::LinearAlgebra::MatrixNorm = MathematicalOperations::Chain< CMath::Sqrt, SquaredMatrixNorm< Matrix > > |
Compute matrix norm 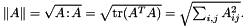 . . | |
| template<class Matrix > | |
| using | RFFGen::LinearAlgebra::GeometricNonlinearity = LeftCauchyGreenStrainTensor< Matrix > |
| Model of the geometric nonlinearity in elasticity theory. Implemented as template-alias to CauchyGreenStrainTensor. | |
| template<class Matrix > | |
| using | RFFGen::LinearAlgebra::Trace = std::conditional_t< Checks::isConstantSizeMatrix< Matrix >(), ConstantSizeTrace< Matrix >, DynamicSizeTrace< Matrix > > |
| Trace of a matrix (sum of diagonal elements). | |
Functions | |
| template<int row, int col, class Matrix , class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>()>, class = Concepts::MatrixConceptCheck<Matrix>> | |
| auto | RFFGen::LinearAlgebra::computeCofactor (Matrix const &A) |
Compute the 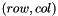 -cofactor of -cofactor of 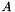 . Implemented for . Implemented for 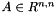 with with 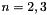 . More... . More... | |
| template<int row, int col, class Matrix , class = std::enable_if_t<!Checks::isConstantSizeMatrix<Matrix>()>, class = std::enable_if_t<Checks::isDynamicMatrix<Matrix>()>, class = Concepts::MatrixConceptCheck<Matrix>> | |
| auto | RFFGen::LinearAlgebra::computeCofactor (Matrix const &A) |
Compute the 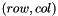 -cofactor of -cofactor of 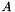 . Implemented for . Implemented for 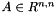 with with 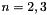 . More... . More... | |
| template<int row, int col, class Matrix , class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>()>, class = Concepts::MatrixConceptCheck<Matrix>> | |
| auto | RFFGen::LinearAlgebra::computeCofactorDirectionalDerivative (Matrix const &A, Matrix const &B) |
Compute the first directional derivative in direction 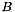 of the of the 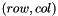 -cofactor of -cofactor of 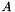 . Implemented for . Implemented for 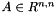 with with 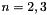 . More... . More... | |
| template<int row, int col, class Matrix , class = std::enable_if_t<!Checks::isConstantSizeMatrix<Matrix>()>, class = std::enable_if_t<Checks::isDynamicMatrix<Matrix>()>, class = Concepts::MatrixConceptCheck<Matrix>> | |
| auto | RFFGen::LinearAlgebra::computeCofactorDirectionalDerivative (Matrix const &A, Matrix const &B) |
Compute the first directional derivative in direction 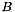 of the of the 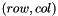 -cofactor of -cofactor of 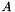 . Implemented for . Implemented for 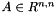 with with 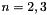 . More... . More... | |
| template<class Matrix > | |
| auto | RFFGen::LinearAlgebra::det (Matrix const &A) |
| Convenient generation of Determinant<Matrix>(A). | |
| template<class Matrix > | |
| auto | RFFGen::LinearAlgebra::determinant (Matrix const &A) |
Convenient computation of 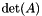 . . | |
| template<class Matrix , class = Concepts::SymmetricMatrixConceptCheck<Matrix>> | |
| auto | RFFGen::LinearAlgebra::deviator (const Matrix &A) |
Deviator of a matrix 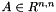 , i.e. , i.e. 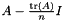 . . | |
| template<class Matrix , class Vector1 , class Vector2 > | |
| Matrix | RFFGen::LinearAlgebra::tensorProduct (const Vector1 &v, const Vector2 &w) |
Compute tensor product 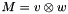 . . | |
| template<class Matrix , class Vector > | |
| Matrix | RFFGen::LinearAlgebra::tensorProduct (const Vector &v) |
Compute tensor product 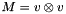 . . | |
| template<class Arg > | |
| auto | RFFGen::LinearAlgebra::trace (const Arg &arg) |
| Convenient generation of Trace<Matrix>. More... | |
| template<class Matrix , class TransposedMatrix = Matrix, class = std::enable_if_t<std::is_same<Matrix,TransposedMatrix>::value>, class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>()>> | |
| TransposedMatrix | RFFGen::LinearAlgebra::transpose (Matrix A) |
| Compute transpose of square matrix. | |
| template<class TransposedMatrix , class Matrix , class = std::enable_if_t<!std::is_same<Matrix,TransposedMatrix>::value>, class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>() && Checks::isConstantSizeMatrix<TransposedMatrix>()>> | |
| TransposedMatrix | RFFGen::LinearAlgebra::transpose (const Matrix &A) |
| Compute transpose of non-square matrix. | |
| template<class Matrix , class = std::enable_if_t<!Checks::isConstantSizeMatrix<Matrix>()>, class = std::enable_if_t<Checks::isDynamicMatrix<Matrix>()>> | |
| Matrix | RFFGen::LinearAlgebra::transpose (Matrix A) |
| Compute transpose of square matrix. | |
| template<class Matrix , class = std::enable_if_t<Checks::isConstantSizeMatrix<Matrix>()>> | |
| Matrix | RFFGen::LinearAlgebra::unitMatrix () |
| Compute unit matrix for the specified constant size matrix type. This requires that a corresponding specialization of Zero is provided. | |
| template<class Matrix , class = std::enable_if_t<!Checks::isConstantSizeMatrix<Matrix>()>> | |
| Matrix | RFFGen::LinearAlgebra::unitMatrix (int rows) |
| Compute unit matrix for the specified dynamic size matrix type. This requires that a corresponding specialization of Zero is provided. | |
Functionality from linear algebra such as (modified) principal and mixed matrix invariants.
| auto RFFGen::LinearAlgebra::computeCofactor | ( | Matrix const & | A | ) |
Compute the 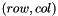 -cofactor of
-cofactor of 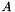 . Implemented for
. Implemented for 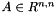 with
with 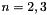 .
.
The 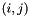 -cofactor of a matrix
-cofactor of a matrix 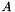 is
is 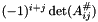 , where
, where 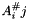 is obtained from
is obtained from 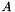 by deleting the
by deleting the 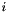 -th row and
-th row and 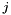 -th column.
-th column.
| auto RFFGen::LinearAlgebra::computeCofactor | ( | Matrix const & | A | ) |
Compute the 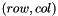 -cofactor of
-cofactor of 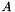 . Implemented for
. Implemented for 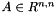 with
with 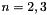 .
.
The 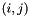 -cofactor of a matrix
-cofactor of a matrix 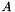 is
is 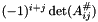 , where
, where 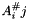 is obtained from
is obtained from 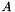 by deleting the
by deleting the 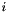 -th row and
-th row and 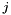 -th column.
-th column.
| auto RFFGen::LinearAlgebra::computeCofactorDirectionalDerivative | ( | Matrix const & | A, |
| Matrix const & | B | ||
| ) |
Compute the first directional derivative in direction 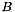 of the
of the 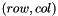 -cofactor of
-cofactor of 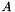 . Implemented for
. Implemented for 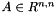 with
with 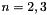 .
.
The 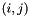 -cofactor of a matrix
-cofactor of a matrix 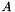 is
is 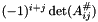 , where
, where 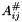 is obtained from
is obtained from 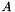 by deleting the
by deleting the 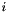 -th row and
-th row and 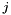 -th column. If
-th column. If 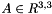 , then the cofactors are quadratic polynomials of the entries of
, then the cofactors are quadratic polynomials of the entries of 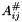 . In this case this function can also used to compute the second directional derivative in directions
. In this case this function can also used to compute the second directional derivative in directions 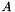 and
and 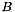 .
.
| auto RFFGen::LinearAlgebra::computeCofactorDirectionalDerivative | ( | Matrix const & | A, |
| Matrix const & | B | ||
| ) |
Compute the first directional derivative in direction 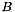 of the
of the 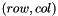 -cofactor of
-cofactor of 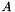 . Implemented for
. Implemented for 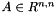 with
with 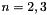 .
.
The 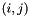 -cofactor of a matrix
-cofactor of a matrix 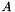 is
is 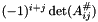 , where
, where 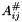 is obtained from
is obtained from 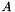 by deleting the
by deleting the 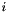 -th row and
-th row and 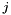 -th column. If
-th column. If 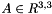 , then the cofactors are quadratic polynomials of the entries of
, then the cofactors are quadratic polynomials of the entries of 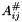 . In this case this function can also used to compute the second directional derivative in directions
. In this case this function can also used to compute the second directional derivative in directions 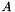 and
and 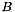 .
.
| auto RFFGen::LinearAlgebra::trace | ( | const Arg & | arg | ) |
Convenient generation of Trace<Matrix>.
 1.8.6
1.8.6